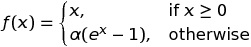In this post we will talk about activation functions, explaining what they are and what are the most commonly used (e.g. ReLU).
Disclaimer: These notes are for the most part a collection of concepts taken from the slides of the ‘Artificial Neural Networks and Deep Learning’ course at Polytechnic of Milan, the book ‘Deep Learning’ (Goodfellow-et-al-2016) and from some other online resources. I am simply putting together all the information to study for the exam and I thought it would be a good idea to upload them here since they can be useful for someone who is interested in this topic.
Activation Functions
There are many design choices that we can take when we are building a parametric machine learning model trained with gradient descent optimization. However, there is one specific design choice which is characteristic of Neural Networks: how to choose the type of hidden unit to use in the hidden layers of the model.
Note:
- The design of hidden units is an extremely active area of research and does not yet have many definitive guiding theoretical principles.
- It is essentially impossible to predict which activation function will work best. The design process consists of trial and error.
Logistic Sigmoid and Hyperbolic Tangent

Why do we like sigmoid function? Essentially because it’s easy to work with and has all the nice properties of activation functions: it’s non-linear, continuously differentiable, monotonic, and has a fixed output range.
However, there is a serious drawback. Unlike piecewise linear units, sigmoidal units saturate across most of their domain—they saturate to a high value when $z$ is very positive, saturate to a low value when $z$ is very negative, and are only strongly sensitive to their input when $z$ is near 0. The widespread saturation of sigmoidal units can make gradient-based learning very difficult (vanishing gradient).
That’s why when a sigmoidal activation function must be used, the hyperbolic tangent activation function typically performs better than the logistic sigmoid. Tanh squashes a real-valued number to the range [-1, 1]. It’s non-linear. But unlike Sigmoid, its output is zero-centered. Therefore, in practice the tanh non-linearity is always preferred to the sigmoid nonlinearity.
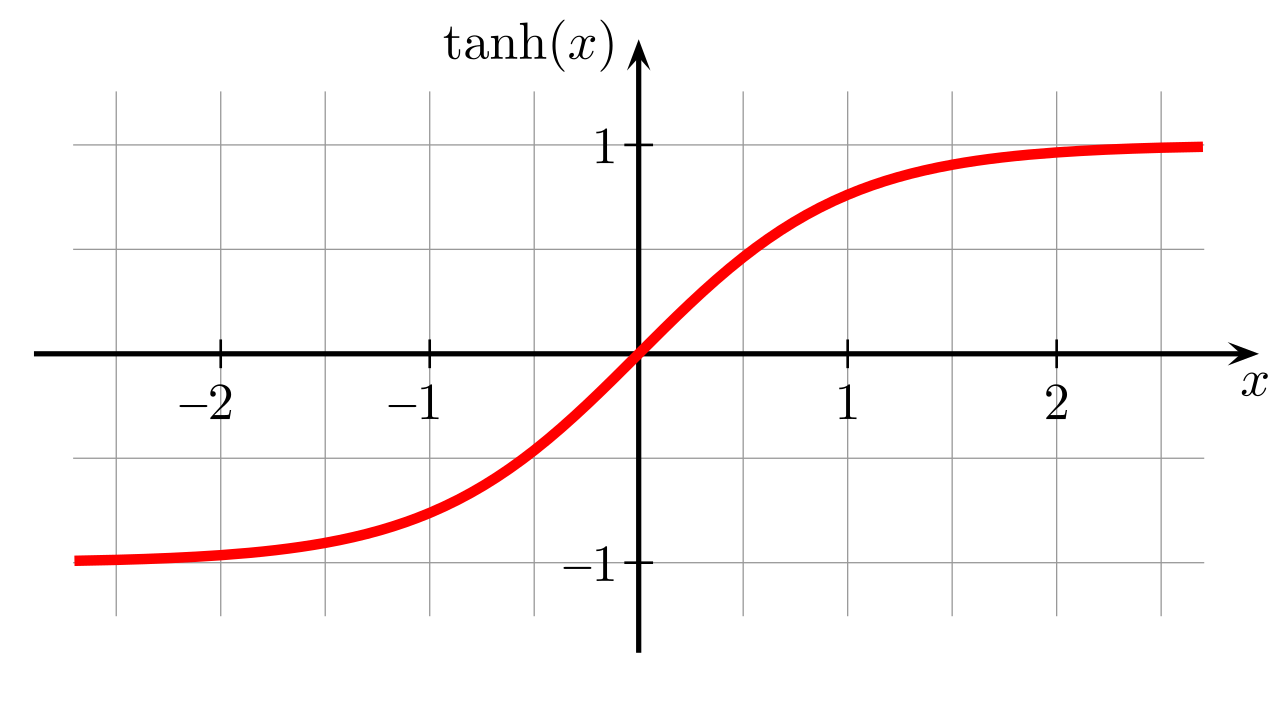
It resembles the identity function more closely, in the sense that $tanh(0) = 0$ while $\sigma(0) = \frac{1}{2}$. For this reason, training a deep neural network with this activation functions resembles training a linear model, thus making the training process easier.
Note however that Tanh still has the vanishing gradient problem.
Rectified Linear Unit (ReLU)
This is nowadays the most used activation function. Despite its name and appearance, it’s not linear and provides the same benefits as Sigmoid but with better performance.
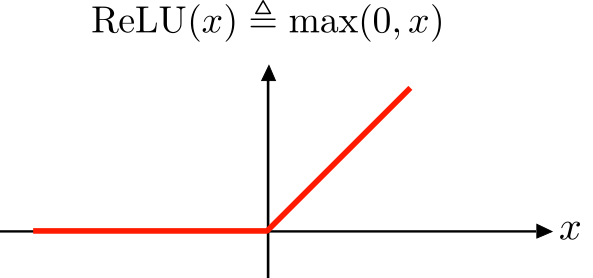
Rectified linear units are easy to optimize because they are so similar to linear units. The only difference between a linear unit and a rectified linear unit is that a rectified linear unit outputs zero across half its domain. This makes the derivatives through a rectified linear unit remain large whenever the unit is active. The gradients are not only large but also consistent.
Pros:
- Faster SGD convergence (6x w.r.t. sigmoid/tanh)
- Sparse activation (only part of the hidden units are activated)
- Efficient gradient propagation (no vanishing or exploding gradient problems), and efficient computation
- Scale-invariant
Of course, there are also possible disadvantages:
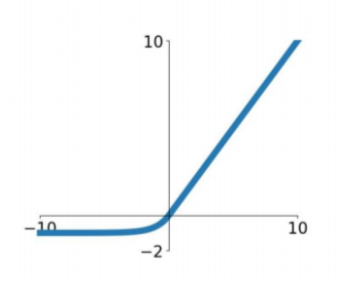
- Non-differentiable at zero; however, it is differentiable anywhere else, and the value of the derivative at zero can be arbitrarily chosen to be 0 or 1.
- The range of ReLu is [0, inf). This means it can blow up the activation.
- For activations in the region $x \le 0$ the gradient will be 0, hence the weights will not get adjusted during descent. The neurons which go in this state will stop responding to variations in error/input, and so they are said to be “died”.
Leaky ReLU and ELU
Leaky ReLUs allow a small, positive gradient when the unit is not active. It is a fix for the “dying ReLU” problem.
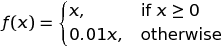
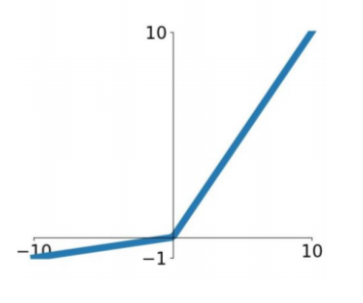
Exponential Linear Unit is a function that tends to converge cost to zero faster and produce more accurate results. Different to other activation functions, ELU has a extra alpha constant which should be positive number (tuned by hand).