Recently we’ve seen researchers and engineers scaling transformer-based models to hundreds of billions of parameters. The transformer architecture is exactly what made this possible, thanks to its sequence parallelism (here is an introduction to the transformer architecture). However, if it certainly enables an efficient training procedure, the same cannot be said about the inference process.
Background
Recall the definition of Attention given in the “Attention Is All You Need” paper:
$$ Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V $$
where $Q$, $K$, and $V$ are three matrices that are trained during the training process. The embeddings of each token (a vector) is multiplied by these three matrices to obtain three vectors $q_n$, $k_n$, and $v_n$.
When computing self-attention, we compute the dot product of the query vector $q_n$ with the key vector of every other token before it in the input sequence ${k_n, k_{n+1}, …, k_N}$.
Each product $q_i^T \cdot k_j$ is divided by the square root of the dimension of the key vectors $\sqrt{d_k}$ in order to have more stable gradients. Eventually, everything is passed through a softmax to normalize the scores:
$$ a_{ij} = \frac{\exp(q_i^T k_j / \sqrt{d_k})}{\sum_{t=1}^{i}\exp(q_i^T k_t / \sqrt{d_k})} $$
The final output is derived by computing the weighted average over the value vectors:
$$ o_i = \sum_{j=1}^{i} a_{ij} v_j $$
The autoregressive nature of transformers
Transfomer-based models are autoregressive models, meaning essentially that they use the past to predict the future.
Given a prompt $(x_1, …, x_n)$
generate vectors k_1, ..., k_n and v_1, ..., v_n
compute the probability of the first new token
Since the tokens $(x_1, …, x_n)$ are all known, computing $P(x_{n+1}|x_1,\dots,x_n)$ can be made with matrix-matrix multiplication and thus benefit from GPU parallelism.
Instead, when we get to compute the remaining tokens $P(x_{n+t+1}|x_1,\dots,x_{n+t})$, the data dependency forces us to use a matrix-vector multiplication, which is less efficient and leads to an underutilization of the GPU.
Reference: Efficient Memory Management for Large Language Model Serving with PagedAttention
The KV cache
In the process we described above, one can notice that the key and value vectors $k_1,\dots,k_{n+t-1}$ and $v_1,\dots,v_{n+t-1}$ seem to be re-computed every time a new token is taken into consideration. Of course, this would be a waste of resources.
Consider the below illustration:
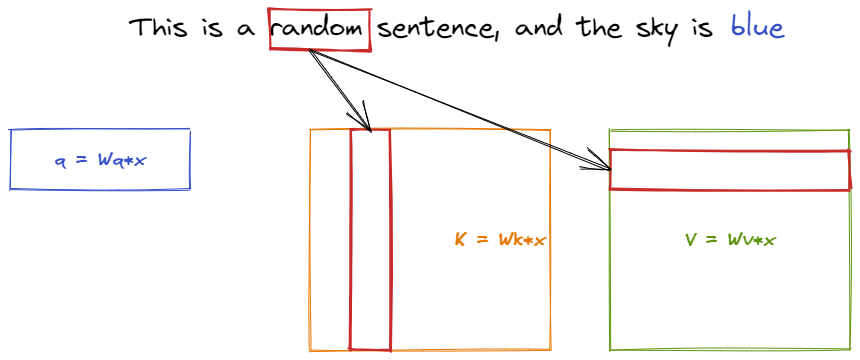
The $K$ and $V$ matrices contain information about all the sequence, while the query vector contains just the information about the last token. The dot product between $q$ and $K$ corresponds to doing attention between the last token (i.e. “blue” in our example) and all the previous ones.
Note two things:
- during the sequence generation one token at a time, the two matrices $K$ and $V$ do not change very much
- once we computed the embedding for the new token, it’s not going to change, no matter how many more tokens we generate
That is why the key and value vectors of existing tokens are often cached for generating future tokens. This approach leads to what is called the KV cache. Note that the KV cache of one token depends on all its previous tokens, hence if we have the same token appearing in two different positions inside the sequence, the corresponding KV caches will be different as well.
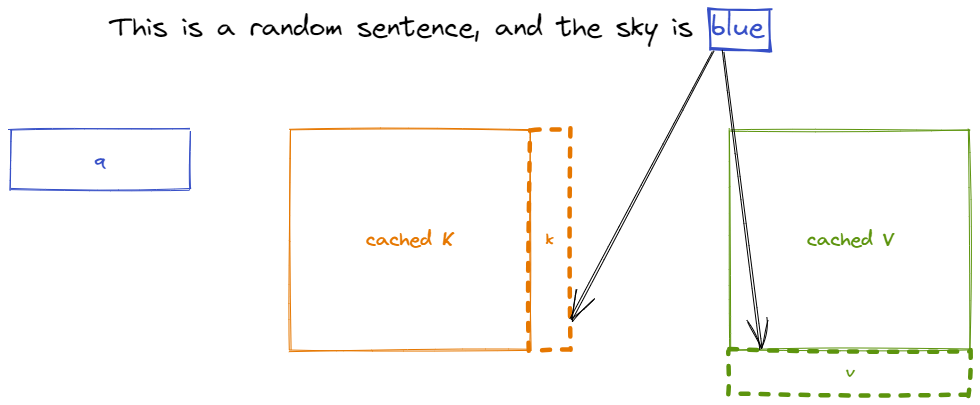
How much memory does KV cache use?
Let’s consider a 13B parameter OPT model
$$ \displaylines{\text{memory_usage_per_token} = \text{num_vectors} * \text{hidden_state_size} * \text{num_layers} * \text{precision (bytes)} \\ = 2 * 5120 * 40 * 2 = 800\; \text{KB}} $$
where $\text{num_vectors}$ refers to the key and value vectors.
In OPT a sequence can be made of up to 2048 tokens, hence we would need $800 * 2048 \approx 1.6\; \text{GB}$ per single request.

A large KV cache is thus a limitation when dealing with LLM inference. Moreover, as pointed out by Kwon et al. in Efficient Memory Management for Large Language Model Serving with PagedAttention, the current trend in the GPU market is characterized by a stable growth in the computation speed (FLOPS) and a much slower increase of the memory capacity. That is why they believe
the memory will become an increasingly significant bottleneck.
In their paper, Kwon et al. proposes a new attention algorithm that is inspired by the paging mechanism of operating systems to efficiently manage KV cache. Their results are quite promising, showing a 2-4x throughput improvements over the SOTA. Check their paper for more details!